Értse meg a szemléletes lencsek geometriáját

Amikor a távcsőtervezők optikai lencsekről beszélnek, egyetlen lencseelemről vagy lencseelemek csoportjáról szólok (Ábra 1). A monolitikus lencsek példái közé tartoznak a síkos-konvex (PCX) lencsek, az egyszeres konvex (DCX) lencsek, az aszférikus lencsek stb. A komponenskomponensek példái közé tartoznak a telecentrikus képalkotó lencsek, a végtelen korrekció útiobjektívek, a sugárcsúsztatók stb. Minden kombináció egy sor lencseelemet tartalmaz, mindegyikkel egy adott lencsegeometriával, amely saját módon vezérli a fényt.

Ábra 1: Síkos-konvex lencse (egyes elem bal oldalon) és telecentrikus képalkotó lencse (elemek kombinációja jobb oldalon)

Snell törési törvénye

Mielőtt belemernénk a lencsegeometria minden típusába, vegyük figyelembe, hogyan sújtják az optikai lencsek a fényt a törés tulajdonságainak segítségével. A törés azt mutatja be, hogy a fény milyen mértékben tér el, amikor belép vagy kilép egy közegből. Az eltérés függ a közeg törésmutatójától és a fény szögét a felület normálisával szemben. Ez a tulajdonság által Snell-törési törvény (egyenlet 1) szabályozott, ahol n1 a befutó közeg törésmutatója, θ1 a befutó fény szöge, n2 a törés közeg indexe, és θ2 a törés fény szöge. A Snell-törési törvény leírja az incidens szög és a továbbítási szög közötti kapcsolatot, ahogy a fény különféle közegeken keresztül halad (Ábra 2).

Snell törési törvénye

Mielőtt belemernénk a lencsegeometria minden típusába, vegyük figyelembe, hogyan sújtják az optikai lencsek a fényt a törés tulajdonságainak segítségével. A törés azt mutatja be, hogy a fény milyen mértékben tér el, amikor belép vagy kilép egy közegből. Az eltérés függ a közeg törésmutatójától és a fény szögét a felület normálisával szemben. Ez a tulajdonság által Snell-törési törvény (egyenlet 1) szabályozott, ahol n1 a befutó közeg törésmutatója, θ1 a befutó fény szöge, n2 a törés közeg indexe, és θ2 a törés fény szöge. A Snell-törési törvény leírja az incidens szög és a továbbítási szög közötti kapcsolatot, ahogy a fény különféle közegeken keresztül halad (Ábra 2).

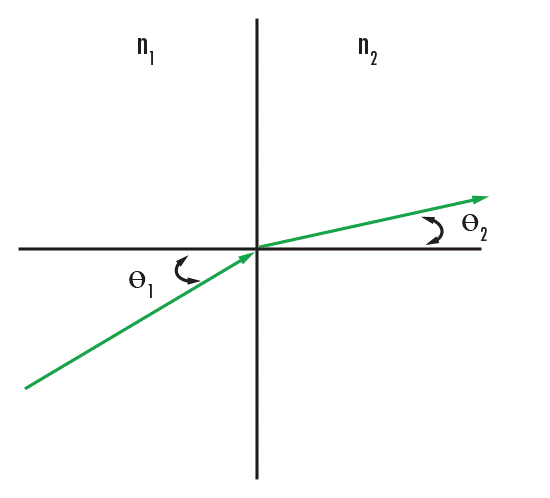
Ábra 2: Snell-törési törvény