Versta de geometrie van optische lenzen

Wanneer optische ontwerpers het hebben over optische lenzen, verwijzen zij naar een enkel lens-element of een groep van lens-elementen (Figuur 1). Voorbeelden van monolitische lenzen zijn vlak-convexe (PCX) lenzen, dubbel-convexe (DCX) lenzen, asferische lenzen, etc. Voorbeelden van componenten zijn telecentrische beeldlenzen, oneindigheidscorrectieobjectieven, straalverlengers, etc. Elk combinatie bestaat uit een reeks van lens-elementen, elk met een specifieke lensgeometrie die licht op eigen wijze controleert.

Figuur 1: Vlak-convexe lens (enkel element links) en telecentrische beeldlens (combinatie van elementen rechts)

Snel's wet van breking

Voordat we ingaan op elk type lensgeometrie, overweeg hoe optische lenzen licht buigen met behulp van de eigenschappen van breking. Breking is de manier waarop licht afwijkt van een bepaalde hoeveelheid wanneer het een medium binnentreedt of verlaat. De afwijking is een functie van de brekingsindex van het medium en de hoek van het licht ten opzichte van de oppervlaknormaal. Deze eigenschap wordt beheerst door Snell's wet van breking (vergelijking 1), waarbij n1 de brekingsindex van het inkomende medium is, θ1 de hoek van het inkomende licht is, n2 de index van het brekende medium is, en θ2 de hoek van het brekende licht is. Snell's wet beschrijft de relatie tussen de invalshoek en de transmissiehoek van licht terwijl het zich voortplant door verschillende media (Figuur 2).

Snel's wet van breking

Voordat we ingaan op elk type lensgeometrie, overweeg hoe optische lenzen licht buigen met behulp van de eigenschappen van breking. Breking is de manier waarop licht afwijkt van een bepaalde hoeveelheid wanneer het een medium binnentreedt of verlaat. De afwijking is een functie van de brekingsindex van het medium en de hoek van het licht ten opzichte van de oppervlaknormaal. Deze eigenschap wordt beheerst door Snell's wet van breking (vergelijking 1), waarbij n1 de brekingsindex van het inkomende medium is, θ1 de hoek van het inkomende licht is, n2 de index van het brekende medium is, en θ2 de hoek van het brekende licht is. Snell's wet beschrijft de relatie tussen de invalshoek en de transmissiehoek van licht terwijl het zich voortplant door verschillende media (Figuur 2).

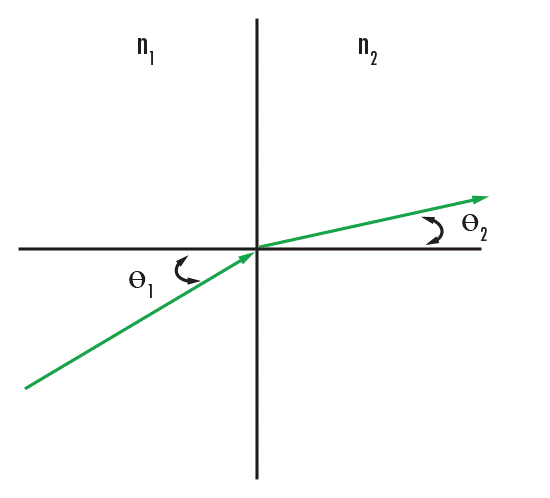
Figuur 2: Snell's wet van breking