Zrozum geometrię soczewek optycznych

Kiedy projektanci optyczni mówią o soczewkach optycznych, odnoszą się do pojedynczego elementu soczewki lub grupy elementów soczewkowych (Rysunek 1). Przykłady monolitycznych soczewek obejmują soczewki płasko-wypukłe (PCX), podwójnie wypukłe (DCX), soczewki asferyczne itp. Przykłady komponentów to soczewki obrazujące telecentryczne, obiektywy z korekcją nieskończonej, rozszerzacze promieni itp. Każdy zestaw składa się z serii elementów soczewkowych, każdy z określonej geometrii soczewki kontrolującej światło na swój sposób.

Rysunek 1: Soczewka płasko-wypukła (pojedynczy element po lewej stronie) i soczewka obrazująca telecentryczna (kombinacja elementów po prawej stronie)

Prawo załamania Snella

Przed zagłębieniem się w każdy rodzaj geometrii soczewki, rozważ, jak soczewki optyczne gią światło za pomocą właściwości załamania. Zalamanie to sposób, w jaki światło odchyla się o określoną ilość, gdy wchodzi lub opuszcza medium. Odchylenie jest funkcją wskaźnika załamania medium oraz Kąta światła względem wektora normalnego powierzchni. Ta własność jest regulowana przez prawo załamania Snella (równanie 1), gdzie n1 to wskaźnik załamania medium nadchodzącego, θ1 to Kąt światła nadchodzącego, n2 to wskaźnik medium załamującego, a θ2 to Kąt światła załamującego się. Prawo Snella opisuje związek między Kątem padania a Kątem przesunięcia światła podczas poruszania się przez różne media (Rysunek 2).

Prawo załamania Snella

Przed zagłębieniem się w każdy rodzaj geometrii soczewki, rozważ, jak soczewki optyczne gią światło za pomocą właściwości załamania. Zalamanie to sposób, w jaki światło odchyla się o określoną ilość, gdy wchodzi lub opuszcza medium. Odchylenie jest funkcją wskaźnika załamania medium oraz Kąta światła względem wektora normalnego powierzchni. Ta własność jest regulowana przez prawo załamania Snella (równanie 1), gdzie n1 to wskaźnik załamania medium nadchodzącego, θ1 to Kąt światła nadchodzącego, n2 to wskaźnik medium załamującego, a θ2 to Kąt światła załamującego się. Prawo Snella opisuje związek między Kątem padania a Kątem przesunięcia światła podczas poruszania się przez różne media (Rysunek 2).

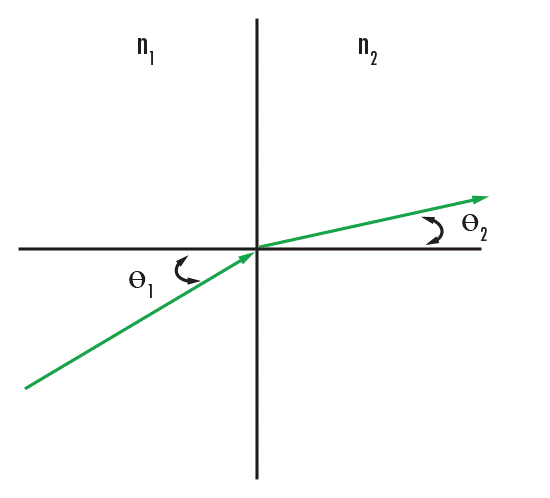
Rysunek 2: Prawo załamania Snella