Розуміння геометрії оптичних лінз

Коли оптичні дизайнери говорять про оптичні лінзи, вони мають на увазі одну лінзову елементу або групу лінзових елементів (Рисунок 1). Приклади монолітних лінз включають плоско-кульмічні (PCX) лінзи, подвійно кульмічні (DCX) лінзи, асферичні лінзи тощо. Приклади складних компонентів - телецентральні відтворювальні лінзи, об'єктиви з коригуванням на нескінченності, розширювачі променів тощо. Кожна комбінація складається з серії лінзових елементів, кожен з яких має певну геометрію лінзи, що керує світлом у власний спосіб.

Рисунок 1: Плоско-кульмічна лінза (один елемент зліва) і телецентральна відтворювальна лінза (комбінація елементів справа)

Закон Сnelle про преломлення

Перш ніж углибитися у кожен тип геометрії лінзи, розгляньте, як оптичні лінзи згиняють світло, використовуючи властивості преломлення. Преломлення - це спосіб, яким світло відхиляється на певну кількість при входженні або виході з середовища. Відхилення є функцією індексу преломлення середовища та кута світла відносно нормалі поверхні. Ця властивість регулюється законом преломлення Снейла (рівняння 1), де n1 - це індекс преломлення входящого середовища, θ1 - це кут входження світла, n2 - це індекс преломлення середовища, а θ2 - це кут преломленого світла. Закон Снейла описує взаємозв'язок між кутом входження та кутом передачі світла при його руху через різні середовища (Рисунок 2).

Закон Сnelle про преломлення

Перш ніж углибитися у кожен тип геометрії лінзи, розгляньте, як оптичні лінзи згиняють світло, використовуючи властивості преломлення. Преломлення - це спосіб, яким світло відхиляється на певну кількість при входженні або виході з середовища. Відхилення є функцією індексу преломлення середовища та кута світла відносно нормалі поверхні. Ця властивість регулюється законом преломлення Снейла (рівняння 1), де n1 - це індекс преломлення входящого середовища, θ1 - це кут входження світла, n2 - це індекс преломлення середовища, а θ2 - це кут преломленого світла. Закон Снейла описує взаємозв'язок між кутом входження та кутом передачі світла при його руху через різні середовища (Рисунок 2).

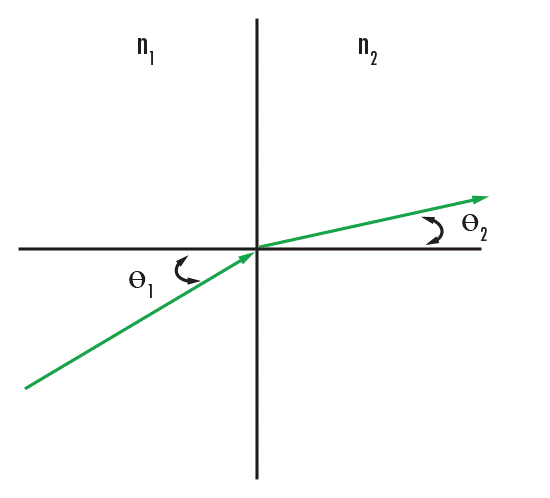
Рисунок 2: Закон преломлення Снейла